Точки перелома производственных возможностей
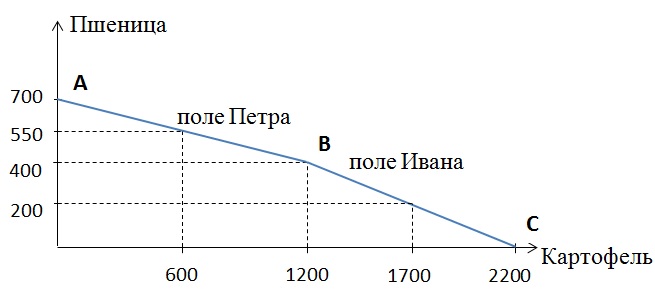
Иван может получить на своем поле либо 400 т пшеницы, либо 1000 т картофеля. Для Петра альтернативной стоимостью выращивания одной тонны картофеля будет производство 0,25 т пшеницы при максимальном урожае картофеля, равном 1200 т. Два фермера – Иван и Петр – решили объединить свои усилия. Это не увеличит их производительности.
а) Построить кривую производственных возможностей «коллективного» хозяйства.
б) Верно ли, что альтернативной стоимостью производства первых 1200 т картофеля является производство 400 т пшеницы?
в) Верно ли, нельзя произвести 600 т картофеля и 550 т пшеницы?
г) Верно ли, что при производстве 1700 т картофеля альтернативной стоимостью увеличения производства картофеля на 20 т является отказ от 8 т пшеницы?
д) Верно ли, что для увеличения производства пшеницы с 200 т на 550 т нужно пожертвовать снижением урожая картофеля на 1100 т.
Решение:
а) Кривая производственных возможностей — это кривая, каждая точка которой показывает все возможные сочетания максимального производства двух экономических благ, в условиях полной занятости ресурсов и неизменной технологии.
Найдём координаты точек перелома:
А: Максимальное производство пшеницы обоих фермеров – 700 тонн. На поле Ивана можно вырастить 400 тонн, на поле Петра – 300 тонн:
1200 × 0,25 = 300.
При этом объём картофеля будет нулевым.
В: Далее определим, на каком из двух полей следует начать выращивать картофель, если фермер решит выращивать хотя бы небольшое его количество.
Для этой цели выберем из двух полей то, на котором выращивание каждой единицы картофеля приведёт к наименьшим потерям объёма пшеницы. То есть выберем то поле, где альтернативные издержки выращивания картофеля наименьшие.
На поле Ивана альтернативные издержки 1 т картофеля равны 0,4 т пшеницы.
А на поле Петра альтернативные издержки 1 т картофеля равны 0,25 т пшеницы.
0,25 меньше чем 0,4, значит, для производства первых тонн картофеля выгоднее использовать поле Петра.
Максимально на его поле можно вырастить 1200 т картофеля, пожертвовав при этом 300 тонн пшеницы.
Точка В будет иметь координаты: 1200 тонн картофеля, 400 тонн пшеницы.
С: Максимальное количество картофеля, которое можно вырастить на двух полях равно 2200 тонн (1000 тонн на поле Ивана и 1200 тонн на поле Петра). При этом объём пшеницы будет нулевым.

б) Неверно, так как альтернативной стоимостью производства первых 1200 т картофеля является производство 300 т пшеницы.
в) Точка, в которой производится 600 тонн картофеля, соответствует верхнему участку КПВ, отражающему производственные возможности поля Петра.
КПВ поля Петра является линейной функцией вида:
Y = a — b × X,
где а — максимально возможный объём пшеницы, когда все ресурсы используются только в производстве пшеницы,
b — коэффициент, характеризующий наклон КПВ и отражающий величину альтернативных издержек выращивания 1 т картофеля.
Итак, КПВ поля Петра описывается уравнением:
Y = 700 — 0,25 × X,
При производстве 600 тонн картофеля можно максимально вырастить:
Y = 700 — 0,25 × 600 = 550 тонн пшеницы.
Таким образом, можно произвести 600 т картофеля и 550 т пшеницы.
г) Точка, в которой производится 1700 т картофеля соответствует нижнему участку КПВ, отражающему производственные возможности поля Ивана.
На поле его поле альтернативные издержки 1 т картофеля равны 0,4 т пшеницы.
Альтернативной стоимостью увеличения производства картофеля на 20 т является отказ от 8 т пшеницы:
8 / 20 = 0,4 т пшеницы — верно.
д) Да, это так.
1700 — 600 = 1100
Источник
Задача 1
Бухгалтеру нужно покрасить свой дом. Для этого он может нанять начинающего маляра, который покрасит дом за 30 рабочих часов и просит за работу 1200 р.
Жена предлагает нашему бухгалтеру покрасить дом самому. Мотивирует она это тем, что бухгалтер в молодости был неплохим маляром. Он затратит на покраску 20 ч. И сэкономит семье деньги.
Бухгалтер завален работой и обычно зарабатывает 100 р. в час. Поэтому он отказывается сам красить дом, ссылаясь на экономическую целесообразность.
Кто прав и почему? Какова цена правильного выбора?
Решение:
Прав бухгалтер. Он сэкономит семье деньги, если будет заниматься своей работой, которая за 20 часов принесёт ему:
20 × 100 = 2000 р.
и наймёт маляра с оплатой 1 200 р.
Цена его выбора, то есть экономия при этом составит:
2 000 – 1 200 = 800 р.
Задача 2
Иванов хочет отремонтировать квартиру. Он может нанять мастеров и заплатить им 15 тыс. р., а может все сделать сам, тогда ремонт будет стоить ему только 5 тыс. р. (цена материалов). Но придется взять отпуск без сохранения заработка. В день он зарабатывает 500 р. Какое максимальное число дней может потратить на ремонт Иванов, чтобы не нести убытки.
Решение:
Пусть x – число дней, потраченных на ремонт.
Если Иванов будет делать ремонт сам, то недополученный заработок составит:
500 × х
И ремонт обойдётся ему в сумму стоимости материалов и недополученного заработка:
500 × х + 5 000.
Чтобы не понести убытки, эта величина должна быть не больше альтернативной стоимости ремонта Иванова — 15 000 р., то есть не больше затрат на оплату труда наёмных мастеров.
Составим и решим неравенство:
500 × х + 5 000 ≤ 15 000
500 × х ≤ 10 000
х ≤ 20.
Итак, Иванов может потратить на ремонт максимум 20 дней.
Задача 3
Петров хочет купить мебельный гарнитур. Он должен затратить на поиски дешевого и качественного варианта 7 рабочих дней, для чего намерен взять отпуск без сохранения заработка. Если он не сделает этого, то купит гарнитур на 20% дороже. В день Петров зарабатывает 1000 руб.
Какова должна быть цена гарнитура для того, чтобы рационально мыслящему Петрову было все равно – искать дешевый вариант или нет?
Решение:
Пусть х – цена гарнитура в рублях.
0,2 * х – величина переплаты, в случае если Петров не возьмёт отпуск.
Если Петров возьмёт отпуск, то потери дохода составят:
7 * 1000 = 7000 р.
Рационально мыслящему Петрову будет все равно – искать дешевый вариант или нет, если величина переплаты будет равна величине потерь дохода.
Составим и решим уравнение:
0,2 * х = 7000
х = 35 000.
Цена гарнитура должна быть равна 35 000 рублей.
Задача 4
Самолетом из Москвы во Владивосток можно добраться за 8 ч, но с учетом сопутствующих затрат времени можно считать, что сутки для работы или отдыха теряются. Поездка в поезде займет 9 дней. Авиабилет стоит 900 р., а железнодорожный билет 500 р.
а) Какой способ передвижения дешевле для человека, зарабатывающего 50 р. каждый рабочий день с понедельника по пятницу.
б) Если 4 из 9 дней пути на поезде приходятся на выходные, то сколько должен зарабатывать в будний день наш путешественник, чтобы ему было все равно с чисто экономической позиции — лететь в выходной день или ехать поездом?
Решение:
а) Для решения данной задачи и подобных задач удобно пользоваться таблицей, в которой сравниваются альтернативные затраты двух способов путешествия.
| Статьи затрат | Самолёт | Поезд |
|---|---|---|
| 1. Недополученный заработок | 50 | 350 |
| 2. Затраты на билет | 900 | 500 |
| ИТОГО | 950 | 850 |
В расчёт недополученного заработка при поездке на поезде берём максимальное из 9 число будних дней, которое может истратить на поездку наш путешественник. Их будет 7. Значит, наибольшие потери дохода за 7 дней составят:
7 × 50 = 350 р.
Следовательно, дешевле ехать поездом.
б) Человеку будет безразлично с чисто экономической позиции — лететь в выходной день или ехать поездом, если альтернативная стоимость полёта на самолёте будет равна альтернативной стоимости поездки на поезде.
Значит, ему должно быть всё равно либо вылететь в субботу, либо выехать в этот день поездом.
Пусть W – дневной заработок в рублях в будний день.
В случае полёта на самолёте он затратит 900 р. Потерь дохода в субботу нет.
При путешествии на поезде затраты составят:
5 * W + 500.
Составим и решим уравнение:
5 * W + 500 = 900
W = 80.
Дневной заработок должен быть равен 80 р., тогда человеку безразлично с экономической точки зрения лететь на самолёте или ехать поездом.
Задача 5
Дедушка, отец и сын организовали семейный бизнес по изготовлению столов и стульев. За год отец может изготовить 50 столов или 100 стульев, дедушка — 40 столов или 100 стульев, сын 100 столов или 150 стульев. Постройте кривую производственных возможностей семьи.
Решение:
Найдём оптимальную структуру производства столов и стульев. Выпуск стульев должен быть поручен тому члену семьи, чьи альтернативные издержки (альтернативная стоимость) выраженные в количестве столов минимальные.
Рассчитаем альтернативную стоимость производства одного стула для каждого члена семьи.
Для дедушки альтернативная стоимость производства одного стула:
40 / 100 = 0,4 стола ← альтернативные издержки минимальные!!!
Для отца альтернативная стоимость производства одного стула:
50 / 100 = 0,5 стола
Для сына альтернативная стоимость производства одного стула:
100 / 150 = 2/3 стола
Если все члены семьи будут производить только столы, они изготовят 190 столов и 0 стульев.
Допустим, они пожелают начать производство стульев. Значит дедушка, у которого альтернативная стоимость производства стульев минимальная, должен производить стулья в количестве 100 штук. Тогда производством столов будут заниматься отец и сын. Они произведут 50 + 100 = 150 штук столов. Координаты точки перелома кривой производственных возможностей: (100 стульев, 150 столов).
Если спрос по стульям не будет удовлетворён, то к их производству подключится отец. Он следующий по возрастанию значения альтернативной стоимости стульев. Вместе с дедушкой отец произведёт 200 штук стульев.
Тогда сын будет один производить столы. И произведёт их в количестве 100 штук.
Координаты ещё одной точки перелома КПВ: (200 стульев, 100 столов).
И наконец, если все участники производства будут изготавливать только стулья, будет произведено 350 стульев и 0 столов.
Изобразим КПВ на графике:
Задача 6
Фирма имеет кривую спроса:
Зная, что P=100, определить изменение дохода при увеличении проданной продукции на одну единицу.
Решение:
Прирост дохода при увеличении проданной продукции на одну единицу называют предельной выручкой (MR — marginal revenue).
Предельная выручка может быть представлена как частная производная общей выручки по количеству товара.
Кроме того цена и объём связаны между собой функциональной зависимостью: Р = f(Q).
Легко заметить, что второе слагаемое в скобках есть обратное значение эластичности спроса:
Определим эластичность спроса по цене:
При P=100
Тогда:
Таким образом, увеличение количества проданной продукции на единицу, уменьшит доход фирмы на 200 единиц.
Задача 7
Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.
а) Как изменилась выручка фирмы?
б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.
Решение:
а) Выручка фирмы рассчитывается по формуле:
Соответственно изменение выручки фирмы в процентном выражении рассчитаем по формуле:
Таким образом, выручка фирмы увеличилась на 60 %.
б) Коэффициент точечной эластичности рассчитаем по формуле, используемой в определении:
Коэффициент эластичности по абсолютной величине больше 1, следовательно спрос эластичен.
Задача 8
Функция задана уравнением
а) Выведите формулу эластичности этого спроса.
б) При какой цене эластичность спроса по цене составит – 0,5?
в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?
Решение:
а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.
В точке (P0,Q0) точечная эластичность вычисляется как
Где
– производная функции спроса в этой точке.
б)
Отсюда:
Р = 133,33
в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.
Задача 9
Определить точечную эластичность спроса, если при снижении цены на 10 %
выручка увеличилась на 8 %.
Решение:
Пусть P– первоначальная цена до её снижения, а Q– величина спроса до снижения цены.
Тогда выручка будет равна:
PQ.
Из условия задачи известно, что цена снизилась на 10%, запишем это как:
ΔP / P = -0,1
А выручка увеличилась на 8%, то есть стала равна:
1,08PQ
По-другому выручку после изменения можно записать как:
0,9P(Q + ΔQ)
Приравняв два последних выражения, получим уравнение:
Разделим обе части уравнения на PQ
Рассчитаем точечную эластичность спроса по формуле
Так как коэффициент точечной эластичности по абсолютной величине больше единицы, следовательно спрос эластичен.
Задача 10
Определить точечную эластичность спроса на товар, если уменьшение цены на 5 % привело к снижению выручки на 2 %.
Решение:
Пусть P– первоначальная цена до её уменьшения,
а Q– величина спроса до уменьшения цены.
Тогда выручка будет равна PQ.
Из условия задачи известно, что цена снизилась на 5%, запишем это как:
ΔP / P = -0,05
А выручка снизилась на 2%, то есть стала равна:
0,98PQ
По-другому выручку после изменения можно записать как:
0,95P(Q+ΔQ)
Приравняв два последних выражения, получим уравнение:
Разделим обе части уравнения на PQ
Рассчитаем точечную эластичность спроса по формуле:
Так как коэффициент точечной эластичности спроса по абсолютной величине меньше единицы, следовательно, спрос неэластичен.
Источник
Задача 1
Бухгалтеру нужно покрасить свой дом. Для этого он может нанять начинающего маляра, который покрасит дом за 30 рабочих часов и просит за работу 1200 р.
Жена предлагает нашему бухгалтеру покрасить дом самому. Мотивирует она это тем, что бухгалтер в молодости был неплохим маляром. Он затратит на покраску 20 ч. И сэкономит семье деньги.
Бухгалтер завален работой и обычно зарабатывает 100 р. в час. Поэтому он отказывается сам красить дом, ссылаясь на экономическую целесообразность.
Кто прав и почему? Какова цена правильного выбора?
Решение:
Прав бухгалтер. Он сэкономит семье деньги, если будет заниматься своей работой, которая за 20 часов принесёт ему:
20 × 100 = 2000 р.
и наймёт маляра с оплатой 1 200 р.
Цена его выбора, то есть экономия при этом составит:
2 000 – 1 200 = 800 р.
Задача 2
Иванов хочет отремонтировать квартиру. Он может нанять мастеров и заплатить им 15 тыс. р., а может все сделать сам, тогда ремонт будет стоить ему только 5 тыс. р. (цена материалов). Но придется взять отпуск без сохранения заработка. В день он зарабатывает 500 р. Какое максимальное число дней может потратить на ремонт Иванов, чтобы не нести убытки.
Решение:
Пусть x – число дней, потраченных на ремонт.
Если Иванов будет делать ремонт сам, то недополученный заработок составит:
500 × х
И ремонт обойдётся ему в сумму стоимости материалов и недополученного заработка:
500 × х + 5 000.
Чтобы не понести убытки, эта величина должна быть не больше альтернативной стоимости ремонта Иванова — 15 000 р., то есть не больше затрат на оплату труда наёмных мастеров.
Составим и решим неравенство:
500 × х + 5 000 ≤ 15 000
500 × х ≤ 10 000
х ≤ 20.
Итак, Иванов может потратить на ремонт максимум 20 дней.
Задача 3
Петров хочет купить мебельный гарнитур. Он должен затратить на поиски дешевого и качественного варианта 7 рабочих дней, для чего намерен взять отпуск без сохранения заработка. Если он не сделает этого, то купит гарнитур на 20% дороже. В день Петров зарабатывает 1000 руб.
Какова должна быть цена гарнитура для того, чтобы рационально мыслящему Петрову было все равно – искать дешевый вариант или нет?
Решение:
Пусть х – цена гарнитура в рублях.
0,2 * х – величина переплаты, в случае если Петров не возьмёт отпуск.
Если Петров возьмёт отпуск, то потери дохода составят:
7 * 1000 = 7000 р.
Рационально мыслящему Петрову будет все равно – искать дешевый вариант или нет, если величина переплаты будет равна величине потерь дохода.
Составим и решим уравнение:
0,2 * х = 7000
х = 35 000.
Цена гарнитура должна быть равна 35 000 рублей.
Задача 4
Самолетом из Москвы во Владивосток можно добраться за 8 ч, но с учетом сопутствующих затрат времени можно считать, что сутки для работы или отдыха теряются. Поездка в поезде займет 9 дней. Авиабилет стоит 900 р., а железнодорожный билет 500 р.
а) Какой способ передвижения дешевле для человека, зарабатывающего 50 р. каждый рабочий день с понедельника по пятницу.
б) Если 4 из 9 дней пути на поезде приходятся на выходные, то сколько должен зарабатывать в будний день наш путешественник, чтобы ему было все равно с чисто экономической позиции — лететь в выходной день или ехать поездом?
Решение:
а) Для решения данной задачи и подобных задач удобно пользоваться таблицей, в которой сравниваются альтернативные затраты двух способов путешествия.
| Статьи затрат | Самолёт | Поезд |
|---|---|---|
| 1. Недополученный заработок | 50 | 350 |
| 2. Затраты на билет | 900 | 500 |
| ИТОГО | 950 | 850 |
В расчёт недополученного заработка при поездке на поезде берём максимальное из 9 число будних дней, которое может истратить на поездку наш путешественник. Их будет 7. Значит, наибольшие потери дохода за 7 дней составят:
7 × 50 = 350 р.
Следовательно, дешевле ехать поездом.
б) Человеку будет безразлично с чисто экономической позиции — лететь в выходной день или ехать поездом, если альтернативная стоимость полёта на самолёте будет равна альтернативной стоимости поездки на поезде.
Значит, ему должно быть всё равно либо вылететь в субботу, либо выехать в этот день поездом.
Пусть W – дневной заработок в рублях в будний день.
В случае полёта на самолёте он затратит 900 р. Потерь дохода в субботу нет.
При путешествии на поезде затраты составят:
5 * W + 500.
Составим и решим уравнение:
5 * W + 500 = 900
W = 80.
Дневной заработок должен быть равен 80 р., тогда человеку безразлично с экономической точки зрения лететь на самолёте или ехать поездом.
Задача 5
Дедушка, отец и сын организовали семейный бизнес по изготовлению столов и стульев. За год отец может изготовить 50 столов или 100 стульев, дедушка — 40 столов или 100 стульев, сын 100 столов или 150 стульев. Постройте кривую производственных возможностей семьи.
Решение:
Найдём оптимальную структуру производства столов и стульев. Выпуск стульев должен быть поручен тому члену семьи, чьи альтернативные издержки (альтернативная стоимость) выраженные в количестве столов минимальные.
Рассчитаем альтернативную стоимость производства одного стула для каждого члена семьи.
Для дедушки альтернативная стоимость производства одного стула:
40 / 100 = 0,4 стола ← альтернативные издержки минимальные!!!
Для отца альтернативная стоимость производства одного стула:
50 / 100 = 0,5 стола
Для сына альтернативная стоимость производства одного стула:
100 / 150 = 2/3 стола
Если все члены семьи будут производить только столы, они изготовят 190 столов и 0 стульев.
Допустим, они пожелают начать производство стульев. Значит дедушка, у которого альтернативная стоимость производства стульев минимальная, должен производить стулья в количестве 100 штук. Тогда производством столов будут заниматься отец и сын. Они произведут 50 + 100 = 150 штук столов. Координаты точки перелома кривой производственных возможностей: (100 стульев, 150 столов).
Если спрос по стульям не будет удовлетворён, то к их производству подключится отец. Он следующий по возрастанию значения альтернативной стоимости стульев. Вместе с дедушкой отец произведёт 200 штук стульев.
Тогда сын будет один производить столы. И произведёт их в количестве 100 штук.
Координаты ещё одной точки перелома КПВ: (200 стульев, 100 столов).
И наконец, если все участники производства будут изготавливать только стулья, будет произведено 350 стульев и 0 столов.
Изобразим КПВ на графике:
Задача 6
Фирма имеет кривую спроса:
Зная, что P=100, определить изменение дохода при увеличении проданной продукции на одну единицу.
Решение:
Прирост дохода при увеличении проданной продукции на одну единицу называют предельной выручкой (MR — marginal revenue).
Предельная выручка может быть представлена как частная производная общей выручки по количеству товара.
Кроме того цена и объём связаны между собой функциональной зависимостью: Р = f(Q).
Легко заметить, что второе слагаемое в скобках есть обратное значение эластичности спроса:
Определим эластичность спроса по цене:
При P=100
Тогда:
Таким образом, увеличение количества проданной продукции на единицу, уменьшит доход фирмы на 200 единиц.
Задача 7
Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.
а) Как изменилась выручка фирмы?
б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.
Решение:
а) Выручка фирмы рассчитывается по формуле:
Соответственно изменение выручки фирмы в процентном выражении рассчитаем по формуле:
Таким образом, выручка фирмы увеличилась на 60 %.
б) Коэффициент точечной эластичности рассчитаем по формуле, используемой в определении:
Коэффициент эластичности по абсолютной величине больше 1, следовательно спрос эластичен.
Задача 8
Функция задана уравнением
а) Выведите формулу эластичности этого спроса.
б) При какой цене эластичность спроса по цене составит – 0,5?
в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?
Решение:
а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.
В точке (P0,Q0) точечная эластичность вычисляется как
Где
– производная функции спроса в этой точке.
б)
Отсюда:
Р = 133,33
в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.
Задача 9
Определить точечную эластичность спроса, если при снижении цены на 10 %
выручка увеличилась на 8 %.
Решение:
Пусть P– первоначальная цена до её снижения, а Q– величина спроса до снижения цены.
Тогда выручка будет равна:
PQ.
Из условия задачи известно, что цена снизилась на 10%, запишем это как:
ΔP / P = -0,1
А выручка увеличилась на 8%, то есть стала равна:
1,08PQ
По-другому выручку после изменения можно записать как:
0,9P(Q + ΔQ)
Приравняв два последних выражения, получим уравнение:
Разделим обе части уравнения на PQ
Рассчитаем точечную эластичность спроса по формуле
Так как коэффициент точечной эластичности по абсолютной величине больше единицы, следовательно спрос эластичен.
Задача 10
Определить точечную эластичность спроса на товар, если уменьшение цены на 5 % привело к снижению выручки на 2 %.
Решение:
Пусть P– первоначальная цена до её уменьшения,
а Q– величина спроса до уменьшения цены.
Тогда выручка будет равна PQ.
Из условия задачи известно, что цена снизилась на 5%, запишем это как:
ΔP / P = -0,05
А выручка снизилась на 2%, то есть стала равна:
0,98PQ
По-другому выручку после изменения можно записать как:
0,95P(Q+ΔQ)
Приравняв два последних выражения, получим уравнение:
Разделим обе части уравнения на PQ
Рассчитаем точечную эластичность спроса по формуле:
Так как коэффициент точечной эластичности спроса по абсолютной величине меньше единицы, следовательно, спрос неэластичен.
