Диффузия в переломах
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 апреля 2020;
проверки требуют 8 правок.
схема осмоса через полупроницаемую мембрану
Диффу́зия (лат. diffusio «распространение, растекание, рассеивание; взаимодействие») — процесс взаимного проникновения молекул или атомов одного вещества между молекулами или атомами другого вещества, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму[1]. В некоторых ситуациях одно из веществ уже имеет выровненную концентрацию и говорят о диффузии одного вещества в другом. При этом перенос вещества происходит из области с высокой концентрацией в область с низкой концентрацией (противоположно направлению вектора градиента концентрации).
Примером диффузии может служить перемешивание газов (например, распространение запахов) или жидкостей (если в воду капнуть чернил, то жидкость через некоторое время станет равномерно окрашенной). Другой пример связан с твёрдым телом: атомы соприкасающихся металлов перемешиваются на границе соприкосновения. Важную роль диффузия частиц играет в физике плазмы.
Скорость протекания диффузии зависит от многих факторов. Так, в случае металлического стержня тепловая диффузия проходит с огромной скоростью. Если же стержень изготовлен из материала с низкой теплопроводностью (например, стекла), тепловая диффузия протекает медленно. Диффузия молекул в общем случае протекает ещё медленнее. Например, если кусочек сахара опустить на дно стакана с водой и воду не перемешивать, то пройдёт несколько недель, прежде чем раствор станет однородным. Ещё медленнее происходит диффузия одного твёрдого вещества в другое. Например, Роберт Бойль показал, что если медь покрыть золотом, то будет происходить диффузия золота в медь. При этом при нормальных условиях (комнатная температура и атмосферное давление) золотосодержащий слой достигнет толщины в несколько микронов только через несколько тысяч лет.[2] Другой пример — систематические исследования диффузии свинца в золото, проведенные Уильямом Робертсом-Остеном и опубликованные в 1896 г. Под грузом за пять лет свинцовый слиток проник в золотой слиток на один миллиметр.[3]
Первое систематическое экспериментальное исследование диффузии было выполнено Томасом Грэмом. Он изучал диффузию в газах, и это явление (Закон Грэма) было описано им в 1831–1833 гг.[4]
Первое количественное описание процессов диффузии было дано немецким физиологом А. Фиком в 1855 году.[3]
Большой вклад в теорию и практику исследования дифузионных процессов внес Я. И. Френкель, предложив и развив в 1926 году идею диффузии локальных дефектов (вакансий и межузельных атомов).[5]
Общее описание[править | править код]
Все виды диффузии подчиняются одним законам. Скорость диффузии пропорциональна площади поперечного сечения образца, а также разности концентраций, температур или зарядов (в случае относительно небольших величин этих параметров). Так, тепло будет в четыре раза быстрее распространяться через стержень диаметром в два сантиметра, чем через стержень диаметром в один сантиметр. Это тепло будет распространяться быстрее, если перепад температур на одном сантиметре будет 10 °C вместо 5 °C. Скорость диффузии пропорциональна также параметру, характеризующему конкретный материал. В случае тепловой диффузии этот параметр называется теплопроводность, в случае потока электрических зарядов — электропроводность. Количество вещества, которое диффундирует в течение определённого времени, и расстояние, проходимое диффундирующим веществом, пропорциональны квадратному корню продолжительности диффузии.
Диффузия представляет собой процесс на молекулярном уровне и определяется случайным характером движения отдельных молекул[6]. Скорость диффузии в связи с этим пропорциональна средней скорости молекул. В случае газов средняя скорость малых молекул больше, а именно она обратно пропорциональна квадратному корню из массы молекулы и растёт с повышением температуры. Диффузионные процессы в твёрдых телах при высоких температурах часто находят практическое применение. Например, в определённых типах электронно-лучевых трубок (ЭЛТ) применяется металлический торий, продиффундировавший через металлический вольфрам при 2000 °C.
Если в смеси газов масса одной молекулы в четыре раза больше другой, то такая молекула передвигается в два раза медленнее по сравнению с её движением в чистом газе. Соответственно, скорость диффузии её также ниже. Эта разница в скорости диффузии лёгких и тяжёлых молекул применяется, чтобы разделять субстанции с различными молекулярными весами. В качестве примера можно привести разделение изотопов. Если газ, содержащий два изотопа, пропускать через пористую мембрану, более лёгкие изотопы проникают через мембрану быстрее, чем тяжёлые. Для лучшего разделения процесс производится в несколько этапов. Этот процесс широко применялся для разделения изотопов урана (отделение 235U от основной массы 238U). Поскольку такой способ разделения требует больших энергетических затрат, были развиты другие, более экономичные способы разделения. Например, широко развито применение термодиффузии в газовой среде. Газ, содержащий смесь изотопов, помещается в камеру, в которой поддерживается пространственный перепад (градиент) температур. При этом тяжёлые изотопы со временем концентрируются в холодной области.
Модели диффузии[править | править код]
Уравнения Фика[править | править код]
С точки зрения термодинамики движущим потенциалом любого выравнивающего процесса является рост энтропии. При постоянных давлении и температуре в роли такого потенциала выступает химический потенциал , обусловливающий поддержание потока вещества. При этом поток частиц вещества пропорционален концентрации и градиенту потенциала:
~
Используя разложение химического потенциала по степеням концентрации, справедливое для газов и слабых растворов,
= …
можно показать, что ведущий член в выражении для потока частиц
которая показывает, что плотность потока вещества (измеренное, например, в моль·см-2с-1) пропорциональна коэффициенту диффузии [см2·с-1] и градиенту концентрации. Это уравнение выражает первый закон Фика. Второй закон Фика связывает пространственное и временно́е изменения концентрации (уравнение диффузии):
Коэффициент диффузии зависит от температуры. В ряде случаев в широком интервале температур эта зависимость представляет собой соотношение Эйнштейна.
Дополнительное поле, наложенное параллельно градиенту химического потенциала, нарушает стационарное состояние. В этом случае диффузионные процессы описываются нелинейным уравнением Фоккера — Планка. Процессы диффузии имеют большое значение в природе:
- питание, дыхание животных и растений;
- проникновение кислорода из крови в ткани человека.
Геометрическое описание уравнения Фика[править | править код]
Во втором уравнении Фика в левой части стоит скорость изменения концентрации во времени, а в правой части уравнения — вторая частная производная, которая выражает пространственное распределение концентрации, в частности, выпуклость функции распределения температуры, проецируемую на ось .
Уравнения Онзагера для многокомпонентной диффузии и термодиффузии[править | править код]
Законы Фика применимы для случая малых значений концентраций и градиентов концентрации .
В 1931 году Ларс Онзагер[7] предложил модель для описания процессов переноса многокомпонентной среды в случае линейных термодинамических неравновесных систем:
Здесь — поток i-й компоненты и — термодинамическая сила, — матрица кинетических коэффициентов.
Термодинамическая сила по Онзагеру определяется как градиент от частной производной энтропии (термин «сила» Онзагер брал в кавычки, поскольку здесь подразумевается «движущая сила»):
где — «термодинамические координаты».
Для тепло- и массопереноса мы можем положить (плотность внутренней энергии) и это концентрация -ой компоненты. Соответствующее значение движущих сил в таком случае выражаются следующим образом:
поскольку
Здесь — температура и — химический потенциал i-й компоненты. Следует отметить, что данное рассмотрение приводится без учета движения среды, поэтому мы здесь пренебрегаем членом с производной давления. Такое рассмотрение возможно в случае малых концентраций примесей с малыми градиентами.
В линейном приближении вблизи точки равновесия мы можем выразить термодинамические силы следующим образом:
Матрица кинетических коэффициентов должна быть симметричной (Теорема Онзагера) и положительно определенной (в случае роста энтропии).
Транспортное уравнение в таком случае может быть записано в следующем виде:
Здесь индексы относятся к внутренней энергии (0) и разным компонентам. Выражение в квадратных скобках является матрицей диффузионных(), термодиффузионных (, ) и температуропроводных () коэффициентов.
В изотермическом случае () и термодинамический потенциал выражается через свободную энергию (или свободную энтропию (англ.)русск.). Термодинамическая движущая сила для изотермичной диффузии определяется отрицательным градиентом химического потенциала , и матрица диффузионных коэффициентов выглядит следующим образом:
().
Существует произвол в выборе определения для термодинамических сил и кинетических коэффициентов, поскольку мы не можем измерить их отдельно, а только их комбинацию . Например, в оригинальной работе Онзагер[7] использовал дополнительный множитель (), тогда как в курсе теоретической физики Ландау и Лифшица[8] этот множитель отсутствует и сила имеет противоположный знак. Это различие можно учесть в формулах для вывода коэффициентов так, что они не повлияют на результаты измерения.
Недиагональная диффузия должна быть нелинейной[править | править код]
Формализм линейной необратимой термодинамики (Онзагера) генерирует систему линейных уравнений диффузии в виде
Если матрица коэффициентов диффузии диагональна, то эта система уравнений является лишь системой независимых уравнений Фика для различных компонент. Предположим, что диффузия не является диагональной, например, , и рассмотрим состояние, в котором . В этом состоянии . Если в некоторой точке то в течение короткого времени становится отрицательным в этой точке. Поэтому линейная недиагональная диффузии не сохраняет положительность концентраций. Недиагональные уравнения многокомпонентной диффузии должны быть нелинейными[9].
Диффузия в пористых средах[править | править код]
См. также[править | править код]
- Диффузия в кристалле
- Диффузия в плазме
- Диффузионное равновесие
- Вращательная диффузия
- Бомовская диффузия
- Осмос
- Солевые пальцы
- Парадокс Гиббса
- Поверхностная диффузия — процесс, связанный с перемещением частиц, происходящий на поверхности конденсированного тела в пределах первого поверхностного слоя атомов (молекул) или поверх этого слоя.
Примечания[править | править код]
- ↑ Б. С. Бокшейн. Атомы блуждают по кристаллу. С. 9—11
- ↑ L.W. Barr (1997), In: Diffusion in Materials, DIMAT 96, ed. H.Mehrer, Chr. Herzig, N.A. Stolwijk, H. Bracht, Scitec Publications, Vol.1, pp. 1–9.
- ↑ 1 2 H. Mehrer. Heroes and Highlights in the History of Diffusion // Diffusion Fundamentals. — 2009. — Т. 11, № 1. — С. 1–32.
- ↑ Diffusion Processes, Thomas Graham Symposium, ed. J.N. Sherwood, A.V. Chadwick, W.M.Muir, F.L. Swinton, Gordon and Breach, London, 1971.
- ↑ Тамм И. Е. Яков Ильич Френкель // Успехи физических наук. — 1962. — Т. LXXVI, № 3. — С. 414.
- ↑ J. Philibert (2005). One and a half century of diffusion: Fick, Einstein, before and beyond. Архивная копия от 13 декабря 2013 на Wayback Machine Diffusion Fundamentals, 2, 1.1-1.10.
- ↑ 1 2 Onsager L. Reciprocal Relations in Irreversible Processes. I (англ.) // Physical Review : journal. — 1931. — Vol. 37, no. 4. — P. 405—426. — doi:10.1103/PhysRev.37.405. — Bibcode: 1931PhRv…37..405O.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2005. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8.
- ↑ A.N. Gorban, H.P. Sargsyan and H.A. Wahab. Quasichemical Models of Multicomponent Nonlinear Diffusion (англ.) // Mathematical Modelling of Natural Phenomena : journal. — 2011. — Vol. 6, no. 5. — P. 184—262. — doi:10.1051/mmnp/20116509.
Литература[править | править код]
- Бокштейн Б. С. Атомы блуждают по кристаллу. — М.: Наука, 1984. — 208 с. — (Библиотечка «Квант». Вып. 28). — 150 000 экз.
Ссылки[править | править код]
- Диффузия примесных атомов на поверхности монокристалла
- Диффузия. Статья из Химической энциклопедии
Источник
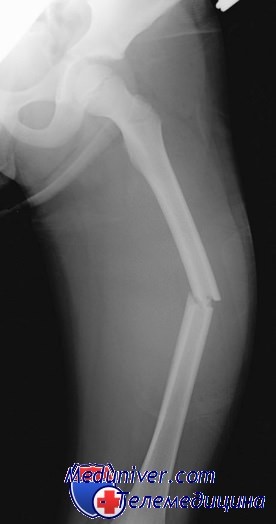
Переломы диафиза бедренной кости. Классификация, диагностика и лечениеДиафиз бедренной кости имеет протяженность от уровня, находящегося на 5 см дистальнее малого вертела, до точки, расположенной на 6 см проксимальнее бугорка, к которому прикрепляется приводящая мышца. Диафиз бедра представляет собой крепкую кость с прекрасным кровоснабжением и, следовательно, хорошей способностью к заживлению. Диафизарные переломы наиболее характерны для детей и подростков. Разгибательная мускулатура, окружающая диафиз, часто служит причиной смещения фрагментов. Мышцы наружной поверхности, прикрепляющиеся к большому вертелу, могут привести к абдукционной деформации, в то время как мышцы, крепящиеся к малому вертелу (подвздошно-поясничная), приводят к наружной ротационно-сгибательной деформации в случае перелома проксимального отдела диафиза бедра. При переломах в средней трети диафиза наблюдается варусная деформация вследствие тяги внутреннего аддуктора, которому оказывают сопротивление наружная группа мышц бедра и широкая фасция.
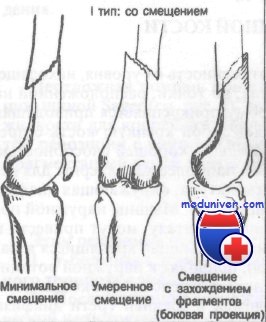
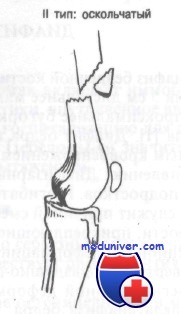
Раньше летальность при переломах диафиза бедра достигала 50%, главным образом из-за длительного пребывания больного в постели. Современное лечение с использованием пластин или интрамедуллярных стержней позволяет рано поднимать больных. Сопутствующие повреждения седалищного нерва при этих переломах наблюдаются редко, благодаря защитному футляру окружающей мускулатуры. Переломы диафиза бедра классифицируют по трем типам: Переломы диафиза бедра обычно являются следствием воздействия значительной травмирующей силы, например при прямом ударе или непрямой передаче силы через согнутое колено.
Больной жалуется на сильную боль в поврежденной конечности, и, как правило, наблюдается заметная деформация последней. Конечность может быть укорочена и при ее движении отмечается крепитация. Бедро может быть отечным и напряженным вследствие кровоизлияния и образования гематомы. Повреждения артерии наблюдаются редко, но вероятность этого следует исключить при первичном обследовании. Повреждение сосудов при переломе диафиза бедренной кости следует заподозрить при: Переломы диафиза бедра обычно являются результатом действия значительной силы. Им могут сопутствовать другие переломы на стороне повреждения, вывихи, повреждения связок и мягких тканей тазобедренного и коленного суставов. Переломы могут сопровождаться ушибами и разрывами мышц в острой стадии с появлением гематомы, а впоследствии с развитием оссифицирующего миозита. Из-за значительной повреждающей силы у многих больных имеются множественные повреждения, требующие тщательного систематического первичного обследования. Переломы диафиза бедра сопровождаются массивным кровотечением, при котором в среднем кровопотеря составляет до 1000 мл.
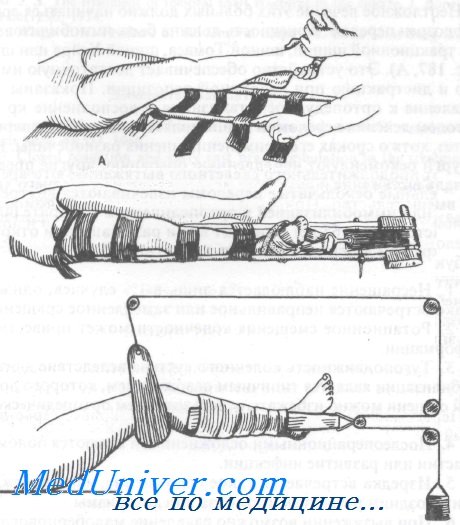
Лечение перелома диафиза бедренной костиНеотложное лечение этих больных должно начинаться сразу же, как заподозрен перелом. Конечность должна быть иммобилизована накожной тракционной шиной, шиной Томаса, шиной Хейра или шиной Sager. Это устройство обеспечивает достаточную иммобилизацию и дистракцию при первичной репозиции. Показаны раннее направление к ортопеду, госпитализация и восполнение кровопотери. Методом лечения переломов I типа является интрамедуллярный остеосинтез, хотя о сроках его применения мнения разноречивы. Некоторые хирурги рекомендуют немедленную операцию, другие предпочитают сначала вытяжение и лишь при безуспешности последнего хирургическое вмешательство. При лечении оскольчатых переломов также нет единой тактики: оно зависит от степени фрагментации и локализации перелома. Переломы проксимального или дистального отдела обычно требуют продолжительного скелетного вытяжения, в то время как незначительные оскольчатые переломы излечиваются внутренней фиксацией или иммобилизацией в ортопедическом аппарате. Больные в возрасте старше 65 лет умирают в три раза чаще при открытом, чем при закрытом лечении переломов этого типа.
Осложнения перелома диафиза бедренной костиПереломам диафиза бедра сопутствует несколько серьезных осложнений. 4. Послеоперационными осложнениями являются поломка гвоздей, пластин или развитие инфекции. — Также рекомендуем «Переломы дистального отдела бедренной кости. Классификация, диагностика и лечение» Оглавление темы «Переломы бедра, костей голени»:
|
Источник